leetcode-23

23. 合并K个升序链表

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

分治和优先队列需要在看一下

示例1：

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

示例2：

输入：lists = []
输出：[]

错误解法

思路1：

先判断非空情况，若不为空，则利用题21的解法依次比较两个链表，实践表明这种方法虽然可以用，但是会超时，解法如下：

class Solution:
    def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
        # printList(l1)
        # printList(l2)
        if l1 == None and l2 == None:
            return None
        elif l1 != None and l2 == None:
            return l1
        elif l1 == None and l2 != None:
            return l2

        if l1.val < l2.val:
            res = ListNode(l1.val)
            l1 = l1.next
        else:
            res = ListNode(l2.val)
            l2 = l2.next
        
        
        p = res
        # 遍历
        while l1 or l2:
            if l1 == None and l2 != None:
                p.next = l2
                break
            elif l2 == None and l1 != None:
                p.next = l1
                break
            else:        
                # print("++")
                if l1.val < l2.val:
                    p.next = ListNode(l1.val) # 链接
                    p = p.next # 指向尾部
                    l1 = l1.next
                else:
                    p.next = ListNode(l2.val)
                    p = p.next
                    l2 = l2.next
        return res
    def mergeKLists(self, lists: List[ListNode]) -> ListNode:
        # print("---")
        # print(lists)
        # print(len(lists))
        # print(type(lists))        
        
        if len(lists) == 0:
            # print("fuck you")
            return None
        elif len(lists) == 1 and type(lists) == None :
            # print(lists[0],type(lists[0]))
            return []
        
        res = lists[0]

        for temp in lists[1:]:
            res = self.mergeTwoLists(res,temp)

        return res

正确解法

需要使用c++

class Solution {
public:
 ListNode* mergeTwoLists(ListNode *a, ListNode *b) {
        // std::cout<<a<<" aa"<<" "<<b<<"bb"<<"\n";
       
        // print(*b)
        if ((!a) || (!b)) return a ? a : b;
        ListNode head, *tail = &head, *aPtr = a, *bPtr = b;
        while (aPtr && bPtr) {
            if (aPtr->val < bPtr->val) {
                tail->next = aPtr; aPtr = aPtr->next;
            } else {
                tail->next = bPtr; bPtr = bPtr->next;
            }
            tail = tail->next;
        }
        tail->next = (aPtr ? aPtr : bPtr);
        return head.next;
    }
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        ListNode *ans = nullptr;
        for (size_t i = 0; i < lists.size(); ++i) {
            ans = mergeTwoLists(ans, lists[i]);
        }
        return ans;
    }
};

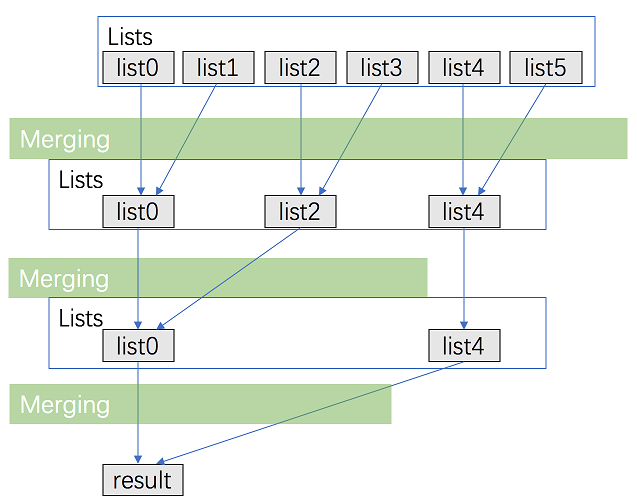
方法二：分治

考虑优化方法一，用分治的方法进行合并。

• 将 $k$ 个链表配对并将同一对中的链表合并；
• 第一轮合并以后，$k$个链表被合并成了$\frac{k}{2}$个链表，平均长度为$\frac{2n}{k}$，然后是$\frac{k}{4}$，$\frac{k}{8}$个链表等等
• 重复这一过程，直到得到了最终的有序链表。

  ListNode* merge(vector <ListNode*> &lists, int l, int r) {
      if(l==r) return lists[l];
      if(l>r) return nullptr;
      int mid = (l+r) >> 1; // 相当于除2
// 递归调用
      return mergeTwoLists(merge(lists,l,mid),merge(lists,mid+1,r));

  }
  ListNode* mergeKLists(vector<ListNode*>& lists) {
      // ListNode *ans = nullptr;
      // for (size_t i = 0; i < lists.size(); ++i) {
      //     ans = mergeTwoLists(ans, lists[i]);
      // }
      // return ans;
      return merge(lists,0,lists.size()-1);
  }

方法三：优先队列

这个方法和前两种方法的思路有所不同，我们需要维护当前每个链表没有被合并的元素的最前面一个，

$k$个链表就最多有$k$个满足这样条件的元素，每次在这些元素里面选取 val 属性最小的元素合并到答案中。

选取最小元素的时候，我们可以用优先队列来优化这个过程。

struct Status {
    int val;
    ListNode *ptr;
    // 重载运算符
    // 返回true时，说明左边形参的优先级低于右边形参
    bool operator < (const Status &rhs) const {
        return val > rhs.val;
    }
};

// 定义优先队列
priority_queue <Status> q;


ListNode* mergeKLists(vector<ListNode*>& lists) {

    // 添加每个链表第一个节点的值和指针
    for (auto node: lists) {
        if (node) q.push({node->val, node});
    }
    ListNode head, *tail = &head;

    // 遍历队列
    while (!q.empty()) {
        auto f = q.top(); q.pop(); // 取第一个元素
        tail->next = f.ptr; // 链接到队头元素 
        tail = tail->next; // 迭代到队头元素
        if (f.ptr->next)    // 添加当前队列的第一个元素 
            q.push({f.ptr->next->val, f.ptr->next});
    }
    return head.next;
}

c++优先队列：

普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。

在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出 （first in, largest out）的行为特征。