边界值分析法

边界值分析法

定义

边界值分析法就是对输入或输出的边界值进行测试的一种黑盒测试方法。

通常边界值分析法是作为对等价类划分法的补充，这种情况下，其测试用例来自等价类的边界。

根据大量的测试统计数据，很多错误是发生在输入或输出范围的边界上，而不是发生在输入/输出范围的中间区域。因此针对各种边界情况设计测试用例，可以查出更多的错误。

设计思路

边界值分析不是从某等价类中随便挑一个典型值或者任意值作为测试数据，而是着重测试已划分出的等价类的每个边界，选取正好等于、刚刚大于或刚刚小于边界的值作为测试数据。

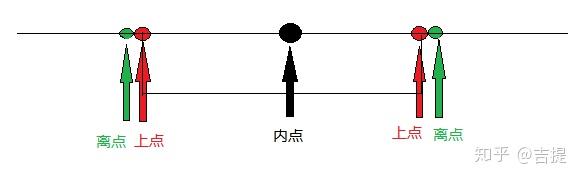
也就是边界值方法中常说的边界5点，即上点、内点和离点。

（1）上点：是指边界上的点，如果域的边界是闭区间的，上点就是在域范围内，如果是开区间的话，上点就是在域范围外。

（2）离点：是指离上点最近的点，如果域的边界是是开区间，那么离点就在范围域内，如果是闭区间，那么离点就在域范围外。

（3）内点：域内的任意一个点都是内点。

小数类型，等价类+边界值测试时的注意事项：
有效等价类：除了有效的小数外，有效的整数也需要测（小数中默认包含了整数，除非需求中明确的说：小数中不包含整数）
无效等价类：小数类型—非小数（非数）：字母、汉字、特殊字符；
		  小数位数—超出小数的有效位数（例如：最多两位，那么>2位就是无效等价类）
边界值：小数的次边界与边界之间的相差单位是与精确度相关的，
例如：精确到小数点后2位，那么相差单位就是0.01。
例如：最小值是：1.00那么次边界就是 0.99 和1.01；
要考虑小数位数的边界问题。例如：小数位数最大值：小数点后2位，那么次边界是：小数点后1位和小数点后3位

边界值分析使用实例

1、测试计算平方根的函数。当输入1个大于等于0的数时，返回其正平方根；当输入一个小于0的数时，提示错误信息Error。

1. 按照等价类划分，得到输入有效等价类为：大于等于0，无效等价类为：小于0。输出有效等价类为大于等于0，无效等价类为Error。

2. 设计测试用例。

   • TestCase1：输入4，输出2。
   • TestCase2：输入-10，提示“Error”。

3. 使用边界值分析方法补充测试用例。分析步骤（1）中的等价类，可知大于等于0的边界值为0，最大正实数，小于0的边界值为0或最小负实数。由此得到以下测试用例。

   • TestCase3：输入最小负实数，提示“Error”。
   • TestCase3：输入绝对值最小负实数，如-0.0001，提示“Error”。
   • TestCase4：输入0，输出0。
   • TestCase5：输入最小实数，如0.0001，输出0.01。
   • TestCase5：输入最大正实数，如1000000，输出,1000。
   • TestCase4：输入0，输出0。

参考文献

1. [ 黑盒测试方法 ] 边界值分析法 - 锅边糊 - 博客园 (cnblogs.com)
2. 《边界值分析》-有这篇就够了 - 知乎 (zhihu.com)